Esta entrada que hoy he decidido escribir, surgió hace ya algún tiempo, como respuesta a un problema cotidiano: tapar mi piscina desmontable y que la cobertura no se hundiera. Para ello, traté de unir los bastidores con una cuerda que bajo la lona, sostuviese a esta. Ahí descubrí (aunque no fuese el primero) una relación entre la Geometría y el Álgebra, que me llenó de satisfacción y que procedo a describir.
Dado un polígono (sea o no regular), se llama polígono estrellado a la poligonal que une todos sus vértices, sin repetir ninguno y que empieza y termina en uno dado (también daría para hablar sobre grafos...).
Por cuestiones estéticas, supongamos que el polígono de partida es regular y que tiene n vértices, al que denotaremos por 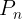 siendo sus vértices
siendo sus vértices 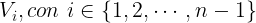 .
.
Si consideramos el conjunto de vértices, podemos definir en él una operación interna, dada por:
Puede comprobarse que al dotar al conjunto de vértices de esta operación e identificar la suma de vértices con una arista, el conjunto pasa a tener estructura de grupo abeliano, y es isomorfo a
Por lo tanto, para cumplir nuestro objetivo, basta con encontrar un generador (o grupo cíclico) del correspondiente Z-módulo. Pero sabemos que la condición necesaria y suficiente para que un elemento 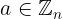 sea un generador es que mcd(a,n)=1. Si a=1 o bien a=n-1, el polígono "estrellado" coincide con el polígono y por lo tanto no será de nuestro "agrado". Usando la notación Schäfli , el polígono que surge en
sea un generador es que mcd(a,n)=1. Si a=1 o bien a=n-1, el polígono "estrellado" coincide con el polígono y por lo tanto no será de nuestro "agrado". Usando la notación Schäfli , el polígono que surge en 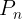 al unir dos vértices a distancia d y lo notaremos {n, d}, es estrellado si y sólo si mcd(n,d)=1.
al unir dos vértices a distancia d y lo notaremos {n, d}, es estrellado si y sólo si mcd(n,d)=1.
¡Una auténtica simbiosis entre la Geometría y el Álgebra! (gracias también por ello, Galois).
En particular, si n es un número primo, al unir vértices con la misma distancia, obtendremos un polígono estrellado (salvo a distancia 1, que como ya hemos comentado, obtendríamos el propio polígono).
Para fijar ideas veamos algunos ejemplos:

Y para que los sentidos se deleiten con bellas construcciones, os dejo este aplet de Geogebra, con el que se puede jugar a mover los deslizadores y probar las propiedades que unen la estas dos disciplinas, en apariencia distantes, como son el Álgebra y la Geometría
Para fijar ideas veamos algunos ejemplos:
- Para n=3, no se pueden trazar otras aristas que las propias del triángulo, con lo que no surge ningún polígono estrellado.
- Para n=4, sólo se tiene la situación no trivial d=2, que nos conduce a una diagonal.
- Para n=5 (primo), los valores d=1, 4 nos conducen las mismo pentágono. En cambio para d=2, 4, tenemos el pentágono estrellado.
- Para n=7, obtenemos dos polígonos estrellados correspondientes a d=2 y 3

Y para que los sentidos se deleiten con bellas construcciones, os dejo este aplet de Geogebra, con el que se puede jugar a mover los deslizadores y probar las propiedades que unen la estas dos disciplinas, en apariencia distantes, como son el Álgebra y la Geometría

Para que aprendamos muchos temas como el de www.mipiscina.com/
ResponderEliminares bueno que continuemos con diversos aspectos que más nos gusten.
Gran ejercicio.
ResponderEliminar-------------------------------------
Trabajo en Colegio del Valle </