El
resultado que da título a esta entrada, ha sido para mí un auténtico
descubrimiento así como un recurso fantástico, que no contemplan los
Decretos que concretan el Currículo, para explicar Geometría en los
primeros cursos de la ESO. Creo fírmemente que debemos conocer al autor, un verdadero desconocido:
Georg Alexander Pick (1859–1942) fue un matemático austriaco nacido en el seno de una familia de origen judío. Su educación inicial estuvo a cargo de su padre hasta que cumplió los 11 años. En 1875 ingresó en la Universidad de Viena y al año siguiente publicó su primer artículo sobre matemáticas, con apenas diecisiete años de edad. Estudió Matemáticas y Física, graduándose en 1879, lo que le permitió tener la formación adecuada para enseñar ambas disciplinas. Tras defender su tesis doctoral, ejerció como asistente en la Universidad Alemana de Praga, en la actual República Checa, donde en 1888 fue nombrado profesor.
Sus 67 publicaciones matemáticas, abordaron distinto campos, siendo su
aportación más importante el llamado Teorema
de Pick, que apareció en un artículo en
1899. Este resultado no tuvo gran notoriedad hasta que el matemático Hugo
Steinhaus Dyonizy lo incluyó en su Mathematical Snapsghots (1969).
Pick fue nombrado rector de la Facultad de
Filosofía de Praga en 1901 En 1910 fue el principal impulsor de la
candidatura a Catedrático de Física de Albert Einstein (cargo que ocupó hasta
1913) y durante estos años los dos se volvieron amigos íntimos tanto por sus
intereses científicos, como por su gran afición por la música.
En 1927
pasó a ser profesor emérito de la Universidad de Praga y abandonó toda
actividad académica. Pick fue elegido miembro de la Academia de Ciencias y
Artes de la República Checa pero los nazis lo excluyeron y enviaron
al campo de concentración de Theresienstadt el 13 de julio de 1942 y murió dos semanas más tarde, a los ochenta y dos años.
 | |||
|
El Teorema de Pick es una
fórmula que nos permite obtener el área de un polígono simple (que no tiene
agujeros ni intersecciones de sus lados). Otra de sus exigencias es que las coordenadas de los puntos donde se
traza el polígono sean enteras (puntos enteros),
es decir en una malla reticular cuadrada.
Sea un polígono simple cuyos
vértices son puntos enteros. Si B es el número de puntos enteros en el
borde, I el número de puntos enteros en el interior del polígono,
entonces el área A del polígono se puede calcular con la fórmula:
|
Ejemplo:
Consideremos el polígono simple
Se observa que el número de puntos en su
interior (marcados en rojo) es 13 y el número de puntos en el
borde
(marcados en azul) es 12. Por lo tanto su área viene dada por:
Símplemente...genial. Con unas hipótesis muy leves, podemos calcular el área de figuras sumamente intrincadas y además de una manera elegante. La demostración del mismo, puede hacerse usando el Principio de Inducción.
Las posibilidades didácticas de este resultado son muy ámplias, pero como es de esperar, no es la panacea. De hecho, la restricción sobre las coordenadas enteras de los vértices hace que no podamos calcular, por ejemplo, el área de un triángulo equilátero (háganse las cuentas y en una de las coordenadas de los vertices tiene que aparecer
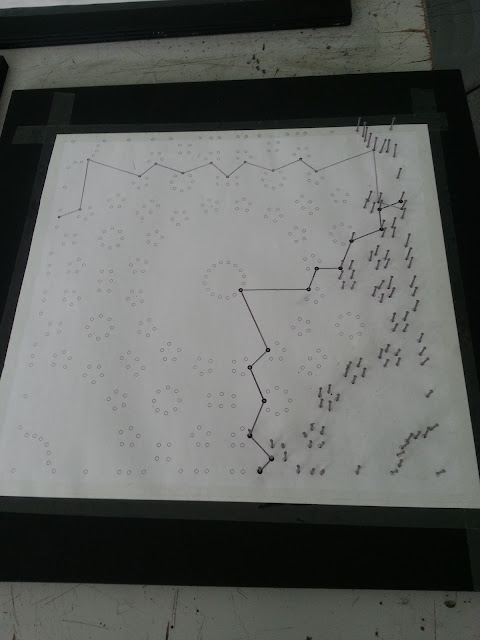
En clase de Tecnología, hemos construidos unos geoplanos con púas y sirviéndonos de lana de colores, realizamos actividades en las que se aplica el resultado de Pick. En la fotografía siguiente, se muestra el ejemplo anterior llevado a la práctica.
Os animo a que realiceis la experiencia, pues si ha ocurrido como en mi caso, ha resultará todo un éxito.
Esta entrada participa en la edición 4.12310562 del Carnaval de Matemáticas, cuyo blog anfitrión es ::ZTFNews.