Esta vez, desde la trinchera del IES Santa María del Águila, he tenido la ocasión de coordinar un programa Andalucía Profundiza titulado Manipulando con las Matemáticas: cúpulas geodésicas.
El alumnado participante han sido 10 chicas y un chico de 3º y 4º de ESO, que cursan Matemáticas Orientadas a las enseñanzas académicas, cuyo interés por el conocimiento y de forma particular por la Matemática, bien merecen el esfuerzo añadido al ya arduo trabajo.
En las 8 sesiones llevadas a cabo durante los meses de abril y mayo, hemos ido desgranando múltiples cuestiones sobre Geometría, cuyo objetivo no era otro que el acercamiento a la consecución última del objetivo: construir cúpulas geodésicas y presentar en distintos concursos (aunque con ópticas diferentes) las ventajas que tienen este tipo de construcciones.
Entrando en materia, una cúpula geodésica es un poliedro construido partiendo de otros (generalmente los sólidos platónicos o regulares) al subdividir sus caras y hacer coincidir los vértices de las nuevas con la esfera circunscrita al poliedro original. La cúpula resultante se clasifica como nV, donde n denota las partes en que se divide la arista original, y es llamada frecuencia de la cúpula.
 |
| Biosphère de Montreal (fuente: Wikipedia) |
Construcción y las Matemáticas que esconde
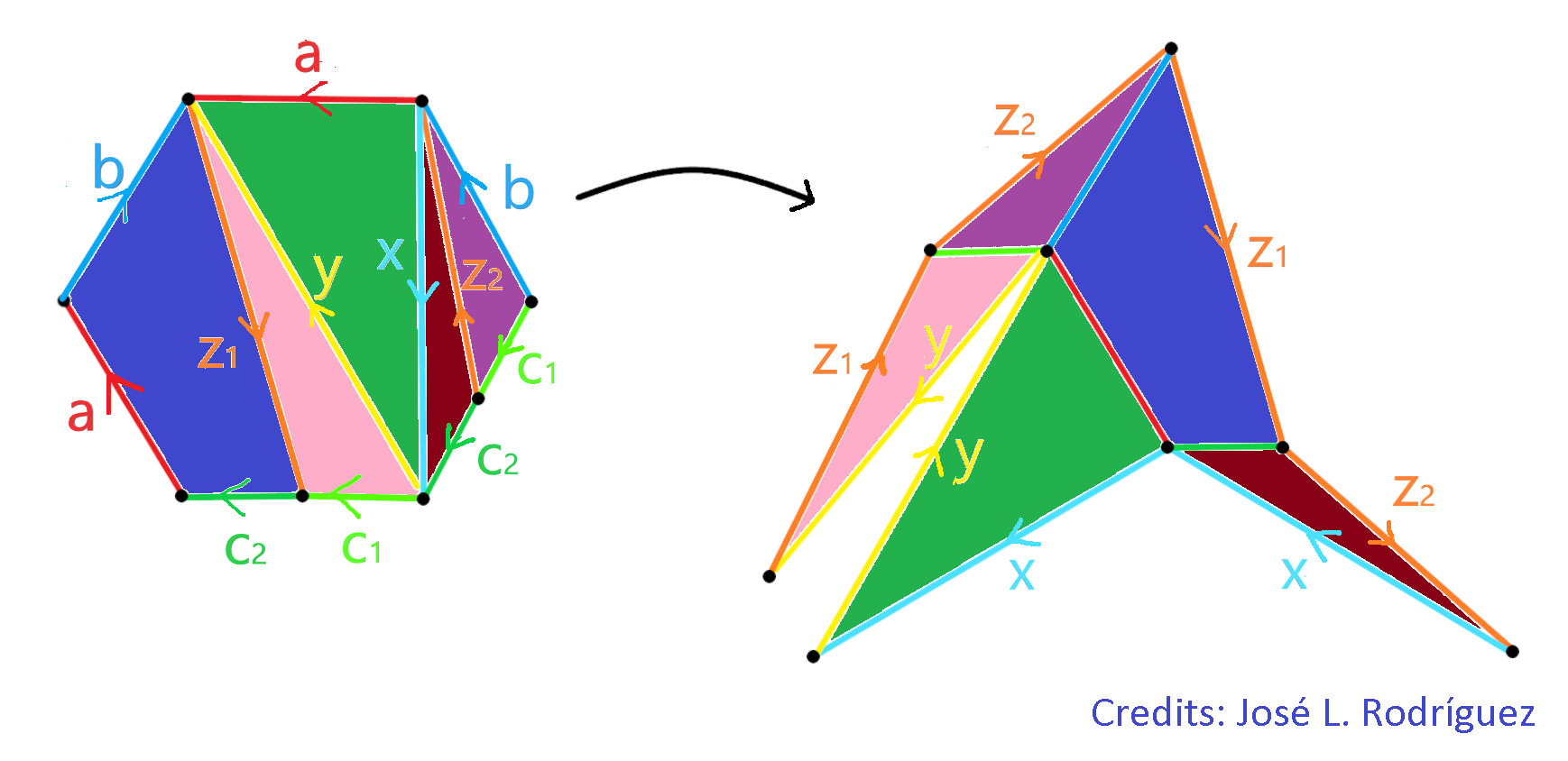
La regularidad del icosaedro, hace que en cara vértice confluyan 5 aristas, de ahí que las que tienen color rojo conserven esa propiedad. Por su parte, las azules inciden en orden 6 (4 azules más 2 rojas) estando relacionadas las Aristas (30 rojas y 35 azules), el número de Vértices (10 de orden 6, 6 de orden 5 y 10 de orden 4) con el número de Caras (30 formadas por triángulos de aristas de distinto color y 10 en color azul) por la fórmula de Euler, para superficies orientables convexas y con un borde:
𝐶 + 𝑉 − 𝐴 = 1 ⇒ 40 + 26 − 65 = 1
El cálculo de la longitud de las aristas rojas y azules, está determinado por el radio R de la esfera circunscrita, e íntimamente ligado al número de oro:
- Tipo B: 35 aristas de 104 cm.
- Tipo A: 30 aristas de 92 cm.
- 10 vértices de orden 4.
- 6 vértices de orden 5.
- 10 vértices de orden 6.
Premio en el VII Certamen de Proyectos Educativos Ambientales de la UAL: Cúpulas geodésicas como viviendas sostenibles.
"contribuir al desarrollo de la alfabetización científica de los estudiantes, así como a la necesidad de difundir y comunicar la ciencia para que los convierta en mejores ciudadanos; fomentar la conciencia ambiental entre los jóvenes; hacerles apreciar el papel fundamental del conocimiento en la conservación del medio ambiente y el desarrollo sostenible del planeta; y apoyar el desarrollo de habilidades transversales de comunicación oral y escrita, fomentando el sentido crítico y la capacidad de trabajo en equipo de los estudiantes."
Este tipo de construcción tiene grandes ventajas desde el punto de vista de una vivienda sostenible:
- La esfera resuelve el problema isoperimétrico, es decir, para un volumen dado, el cuerpo que minimiza el área que encierra es la esfera. Este hecho faculta a las esferas y de forma particular a las cúpulas geodésicas, a convertirse en estructuras que optimizan el material constructivo necesario para su realización.
- La posibilidad de cubrir grandes distancias (recordemos que la Biosphère tiene 76 m de diámetro y 41,5 m de altura) sin el empleo de pilares, hace de su interior un espacio diáfano y versátil que puede ser adaptado a distintos usos y cuya posterior reforma no implica quebraderos de cabeza estructurales a la hora de demoler paredes o encontrarse con incómodas estructuras de hormigón que cercenen las necesidades futuras.
- Suponen un considerable ahorro su construcción en tanto en cuanto los cimientos que requieren no son especialmente sobredimensionados, ni necesitan una roturación grande del terreno donde se vaya a situar.
- Las
cúpulas geodésicas tienen todas las orientaciones posibles, lo que minimiza el
coste energético necesario para obtener un confort climático adecuado, con una
temperatura casi uniforme todo el año. Además, se pueden incorporar sencillos
sistemas de ventilación que permite una climatización geotérmica. Este es el
caso de los pozos canadienses, que se encuentran formados por tuberías
enterradas en el suelo a unos dos metros de profundidad, y que por el principio
de inercia térmica consiguen, dependiendo de la zona climática, que la vivienda
tenga un rango de temperatura en torno a los 20 º C en cualquier estación del
año, sin consumir un solo kilovatio.(Dibujo de la alumna Asmae Errossafi, de un pozo canadiense)
- Se pueden utilizar materiales naturales en su construcción, que garanticen un entorno sostenible. Algunos ejemplos destacados son la celulosa natural como aislante térmico, mortero de cal o corcho natural como envolvente, madera en estructura y cerramientos, paneles solares fotovoltaicos como recubrimientos para la obtención de agua caliente, baterías para almacenar electricidad y canalones o sumideros como sistemas de reciclaje del agua de lluvia.
- Las ventajas aerodinámicas frente a las paredes planas convencionales que conforman los paramentos de las viviendas tradicionales, convierten a las cúpulas geodésicas en estructuras que pueden soportar mejor los envites de los vientos huracanados (nótese que los iglús, variantes de las cúpulas, han sido usados durante siglos como refugios temporales de los pueblos que habitan las regiones más hostiles del hemisferio norte).